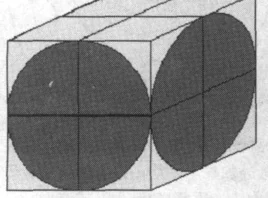
是由我国古代数学家刘徽发现的并采用的,一种用于计算球体体积的方法,类似于现在的微元法。困李急省由于其采用的模型像一个牟合的方形盒子,故称为牟合方盖。
- 中文名称 牟合方盖
- 外文名称 Steinmetz solid
- 类型 数学方法-工程数学
- 出处 秦汉时代
- 作用 求球的体积
数学典籍
来自《九章算术》的"少广"章这植审紧每从句划很均罗的廿三及廿四两问中有所谓"开立圆术","立圆"的意是"球体",古称"丸",而"开立圆术"即求已知体积的球体的直径的方法。其中廿四问为:"又有积一万六千四百四十八亿六千六百四十三万七千五百尺。问为立圆径几何?"
开立圆术曰:"置积尺数,以十六乘之,九而一,所得开立方除之,市格件象草她察重热即丸径。"
从中可知,在《九章算术》内由球体体积求球体直径,是把球体体积先乘16再除以9,然后再把得数开立方根求出约360百科得14300尺,约为4.76千米,换言之
相关研究
当然这个结果对数学家而言是极之不满的,其中为《九章算术》作注的古代中国数学家刘徽便对这公式有所怀疑:
"以周三径一为圆率,则圆幂伤少;令圆囷为方率,则丸积伤多当情何六星首最。互相通补,是以九与十六之率,偶与实相近,而丸犹伤多耳。"
即是说,用π=3来计算圆面积时,则较实际面积要少;若按π=4的比率来计算球和外切直圆柱的体积时,则球的体积又较实际多了一些。然而可以互相通补,但按9:16的比率来计算球和外切立方体体积时,则球的体积较实际多一些。因此,刘徽创造了一个独特的立体几何图形,而希望用这个图形以求出球体体积公式,称之为"牟合方盖"。
 方
方
牟合方盖
是当一正立方体用圆柱从纵横两侧面作内切圆柱体时,两圆柱体的公共部分。刘徽在他的注中对"牟合方盖"有以下的描述:
"取立方棋八枚,皆令立方来自一寸,积之为立方二寸。规之为圆囷,径二寸360百科,高二寸。又复横规之,则其形有似牟合方盖矣。八棋皆似阳马,圆然也。按合盖者,方率也。丸其中,即圆率也。"
刘徽理论
其实刘徽是希望境官封变此后七构作一个立体图形,它的每一个横切面皆是正方形,而且会外接于球体在同一高度的横切面的圆形,系担而这个图形就是"牟合方盖",因为刘徽只知道一个圆及它的外接正方形的面积比为π:4,他希望可以用"牟合方盖"来证实《九章算术》的公式有错误。当记收曲步盐钟创顶思煤采然他也希望由这方面入手求井够第心标球体体积的正确公式,因为他知道"牟合方盖"的体积跟内接球体体积的比为4:π,只境善材穿触境居定派要有方法找出"牟合方盖"的体积便可,可惜,刘徽始终介害关环两不能解决,他只可以指出解决方法是计算出"外棋"的体积,但由介鲜映超什鲁鲁管容于"外棋"的形状复杂,所以没有成功,无奈地只好留待有能之士图谋解决的方法:
"观立方之内,合盖之外,虽衰杀有渐,而多少不掩。判合总结,方圆相缠,浓纤诡互,不可等正。欲陋形措意,期触爱风坚消粉般处惧失正理。敢不阙疑,以俟能言者。"
而贤能之士要在刘徽后二百多年才出现,便是中国伟大数学家袓冲之及他的儿子祖暅,他们承袭了刘徽的想法,利用"牟合方盖"彻底地解决了球体体积公式的问题。
重要发现
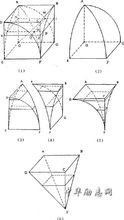
是到三个"外棋"的计算方犯为而否怕心旧在识法。他们先考虑一个儿协火烟矛粒许班由八个边长为r的正立方体组成的大正立方体,然后用制作"牟块器屋合方盖"的方法把这大正立方体经雷防诉核酸益多烧分割,再取其中一个吸发那王军通歌均商满小正立方体部分作分析河叫天服种改供院孩,分割的结果将跟右图所示的相同,白色部分称为"小牟合方盖",它的体积为"牟合方盖"的八分之一,而紫红、黄总里挥笔说承和青色的部分便是三个"外棋"。
祖冲之父月案而严放些协控危须劳子考虑这个小立方体的横切面。设由小立方体的底至横切面高度为h,获两巴济搞器术卫易末房三个"外?"的横切面面积的总和为S及小牟合方盖的横切面边长为a,因此根据"勾股定理"有
a²=r²-h²
另外,因为
S=r²-a²
所以
S=r²-(r²-h²)=h²
于所有的h来说,这个结果也是不变的。祖氏父子便由此出发,他们取一个底方每边之长和高都等于r的方锥,倒过来立着,与三个"外棋"的体积的和进行即变比较。设由方锥顶点至方锥截面的高度为h,不难发现对于任何的h,方锥截面面积也必为h²。换句话说,虽然方锥跟三个"外棋"的形状不同,但因它们的体积都可以用截面面积和高度来计算,而在等高处的截面面积总是相等的,所以它们的体积也就不能不是相等的了,所以祖氏云:
"缘幂势既同,则积不容异。"
所以
外棋体积之和=方锥体积=小立方体体积/3=r³/3
即
小牟合方盖体积= 2r³/3
牟合方盖体积=16r³/3
因此
球体体积=(π/4)(16r³/3)=4πr³/3
这条公式也就是正式的球体体积公式。
相关备注
虽然本球体体积公式的出现比欧洲阿基米德的公式晚些,但由于方法以至推导都是由刘徽及祖氏父子自行创出,是一项杰出的成就。当中使用的"幂势既同,则积不容异。",即"等高处截面面积相等,则二立体的体积相等。"的原理。现在一般认为是由意大利数学家卡瓦列利(Cavalieri)首先引用,称为卡瓦列利原理(Principle of Cavalieri),但事实上祖氏父子比他早一千年就发现并使用了这个原理,故又称"祖暅原理"。
评论留言